Zombies

Source

If I have to explain what differential equations are, I always use the zombie apocalypse as an example. People seem to understand that better than the popular Lotka-Volterra equations modeling predator-prey dynamics, despite the fact that the zombie equations of Munz et al. are much more complicated. Well, to be eaten alive by an undead is just much more scary than being eaten by, say, a lion.

Both the Lotka-Volterra and the Munz models constitute a system of nonlinear coupled differential equations for which no analytical solutions exist. We thus have to solve these equations numerically, which is possible, for example, by pylab.

The basic code to solve the Munz model is simple and short:

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# zombie apocalypse modeling
from pylab import *
from scipy.integrate import odeint
params = {'text.usetex': True,'font.family': 'serif','font.size': 20}
rcParams.update(params)
P = 10      # birth rate
d = 0.0001  # natural death rate
B = 0.0095  # infection rate
G = 0.0001  # resurrection rate
A = 0.02    # killing rate
# solve the system dy/dt = f(y, t)
def f(y, t):
        Si = y[0]
        Zi = y[1]
        Ri = y[2]
        # the model equations (see Munz et al. 2009)
        f0 = P - B*Si*Zi - d*Si
        f1 = B*Si*Zi + G*Ri - Si*Zi
        f2 = d*Si + Si*Zi - G*Ri
        return [f0, f1, f2]
# initial conditions
S0 = 500.                   # initial population
Z0 = 0                      # initial zombie population
R0 = 0.01*S0                # initial death population
y0 = [S0, Z0, R0]           # initial condition vector
t  = linspace(0, 50., 10000)    # time grid
# solve the DEs
soln = odeint(f, y0, t)
S = soln[:, 0]
Z = soln[:, 1]
R = soln[:, 2]
# plot results
figure()
plot(t, S, linewidth=3, label='Living')
plot(t, Z, linewidth=3, label='Zombies')
xlabel('Days from outbreak')
ylabel('Population')
title('Zombies in Peaceville: Apocalypse')
legend(loc=0)
show()

The situation in Peaceville is discouraging. People are doomed:

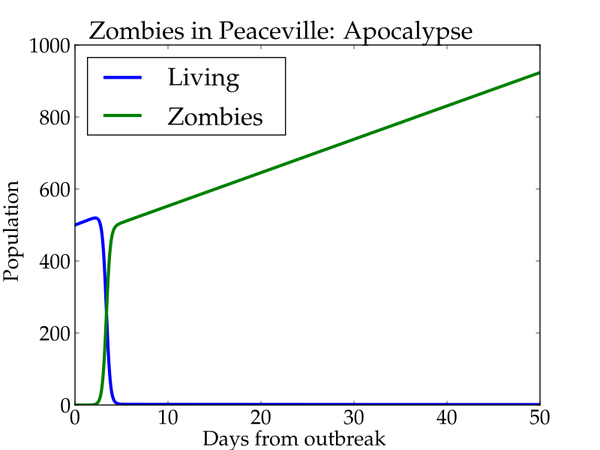
Zombies in Peaceville

Do we stand any chance at all against zombies? But of course we do! With the right spirit we fight them back and eliminate them from the face of the earth: 😉

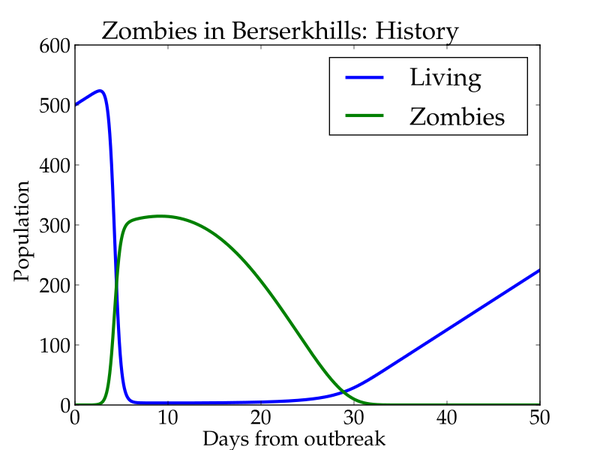
Zombies in Berserkhill

What makes the difference is the resistance the people in Peaceville and Berserkhill offer:

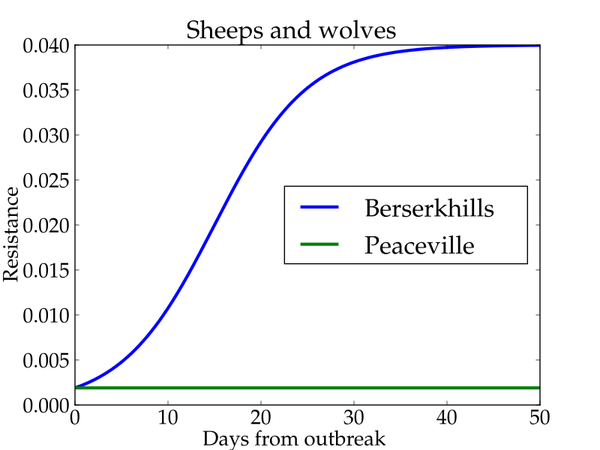
Resistance is the key

What do we learn from that? Even apparently lost fights can be won by determination.