Having fun with classical ciphers
19.12.2013
I've written most of what follows three years ago, but I've never found the time to finish and post it. As usual this close to Christmas, I have a few days off, and took the opportunity to delve once again into the fascinating world of classical ciphers. :cheesey:
27.12.2010
The millenia-old war between code-makers and code-breakers has essentially stopped in the last century: modern ciphers are so strong that they just can't be broken in any humanly accessible time-span. Diffie, Hellmann, and Merkle solved the key exchange problem, Phil Zimmermann gave encryption to the masses, and the GnuPG project transferred Zimmermanns 'Pretty Good Privacy' to the open source world.
End of story. Or is it?
Well, for most practical applications, that's basically it. We can trust that either of the following commands
gpg -ca --passphrase-repeat 0 --cipher-algo aes256 <file> gpg -sea -r cobra <file>
results in an encrypted file whose content will be inaccessible to even the most nosy of our sniffing and snooping friends. Unless, of course, they revert to alternative ways of collecting information. :P
People had this particular problem since the beginning of time and invented steganography. Nowadays, one can can easily hide and encrypt information in one and the same command:
steghide embed -e rijndael-256 -z 9 -cf <coverfile> -ef <embeddedfile>; -sf <combinedfile>
All right, so where's the catch?
My itch with modern ciphers is not a practical one. I rather find their mathematical foundation abstract and dry, although I can digest most of it when I try really hard. However, you can't possibly utilize modern encryption without a computer.
Ancient ciphers, in contrast, are often intuitive and easy to master by paper and pencil. And what's more, ancient ciphers are surrounded by a mystical and glorious aura. Just think of the Enigma!
When I was a kid, Diffie and Hellman as well as Rivest, Shamir and Adleman still chased attractive female students across the campus. There was no modern cryptography, just an afterglow from the war. There were only a handful of computers, and hardly any of them in public possession. Being a nerdy kid, I became member of the local chess club with age eight. People there talked a lot about chess, but also about encryption, and the atmosphere turned out to be infectious. I adored Edgar Allan Poes Gold Bug as well as Arthur Conan Doyles Adventure of the Dancing Men. I was thrilled to death by Vigenère's Le chiffre indéchiffrable (French for 'the indecipherable cipher'). And I would have died for book ciphers. The unbreakable type, you know.
And now over Christmas, I thought, aw what the hell ... let's just play with all that's fun! Being fascinated by the Vigenère cipher, I sat down and implemented it using the only programming language I've ever learned: Pascal. And since we don't have to fill the _tabula recta _ourselves anymore, I've generalized the classical scheme to the entire 95 letter alphabet of the ASCII printable characters. That took me an entire day, but my Pascal courses took place almost 30 years ago. 😞
A Vigenère cipher can be as strong as desired. If the key is as long as the message, and truly random, it constitutes an example of a one-time pad (OTP), the only cipher which is information-theoretically proven to be unbreakable. Despite of this fact, OTPs have been rarely used in the past since key distribution proved to be an insurmountable problem.
Quantum key distribution has solved this problem in principle, but is not (yet) for everyone. Still, if the number of people on a communication channel is limited, the distribution of an OTP is easier than ever. Remember than one A4 page of text roughly corresponds to 3 kB. The 2 GB of an average USB stick would thus suffice for 700,000 of such pages, which should be enough for even the most communicative individuals. 😉
True randomness, however, is an requirement not easily obtained at all, since only natural phenomena such as atmospheric noise or radioactive decay are truly random. A computer, instead, is a deterministic beast and can only generate pseudo-random numbers. The "best" algorithms for doing that are called 'cryptographically secure pseudo-random number generators' (CSPRNG), but even these are predictable to a certain degree. I consider the one I'll use in the following to be a very solid contender, but not necessarily the best (for which Blum-Blum-Shub generators may qualify, though they are slow, and there's no readily available open-source implementation anyway).
How do we judge the quality of a CSPRNG? One of the most popular battery of tests are compiled in the dieharder suite, a successor of George Marsaglia's famous diehard tests. This suite interfaces to the continuous stream of random numbers of the generator, here csrng, like that:
csprng-generate | dieharder -g 200 -a
Two tests were indicated as "weak", but that turned out to be a result of the limited statistics with the default settings of dieharder.
We can also examine a finite list of random numbers created by such a generator. An infinite perfectly random sequence would exhibit an entropy per character equal to S=log2(k), where k is the character space. We will come back to that later.
A Vigenère cipher used in conjunction with a pad generated by a CSPRNG is an example for a running key cipher, but one could equally well call it a pseudo one-time pad (POTP). Depending on the cryptographic quality of the CSPRNG used, it may be trivial or essentially impossible to break. It will never be an information-theoretical secure system such as the OTP, but it may approach a level of security similar to that offered by modern cryptographic techniques.
My little Pascal routine in conjunction with the POTP created by csrng is perfectly capable of encrypting pure ASCII data, but can't handle anything beyond such as extended ASCII, UTF-8 or binary data. To improve on that, I preprocess the 'plaintext' (which may also be an image or an executable) with base91 to obtain a well-defined character set regardless of the file type.
Finally, I need to cut a section of the POTP serving as the key for each respective message, and to subsequently shred this section so it cannot be used again. All of that is easily done by a short shell script. Let's examine the essential ingredients of this script (in pseudo script code, for the actual one, see below):
csprng-generate -n 4G | tr -cd '[:graph:]' | fold -w 65 > POTP
Creates a stream of random numbers with a total volume of 4 GB. The binary stream is filtered through 'tr', letting pass only printable ASCII characters. These characters are then arranged in lines of 65 characters length and saved as our POTP. On my desktop, this command takes about 35 s to complete.
Let's now look at the encryption part (decryption is largely the same, just the order is different):
b91enc -w 65 PLAINTEXT -o ENCODEDTEXT
Encodes the PLAINTEXT with base91, and ensures that the ENCODEDTEXT has the same format as the POTP or the key.
tail -n NUMBER POPT > KEY
Generates the key (NUMBER is determined by the length of the ENCODEDTEXT, see the shell script for details).
vig -e ENCODEDTEXT KEY > ENCRYPTEDTEXT
Encrypts.
truncate -s KEY POTP
Removes the KEY from the POTP.
All of that is pretty straightforward except for the strange fact that I get the KEY from the bottom of the file rather than from the top, which would be the intuitive choice for a 'pad'. The reason for this choice is very simple: removing the key from the bottom takes 1 ms, but from the top several seconds depending on the speed of the hard disk. This asymmetry is an inevitable consequence of the file system's way to store data. With the present 'backward' scheme, the total time for the steps 1. — 4. amounts to 30 (450) ms for an A4 text page (a 5MB pdf).
Let's examine the files created by these steps using John Walker's entropy estimator ent. For the 95 characters used here, a perfectly random and infinite sequence of numbers is expected to have an entropy of 6.570 bit per character. For our POTP as well as for the plaintext encrypted with it, ent arrives at an entropy of 6.569 bits per character.
That's pretty satisfactory, but let's have a closer look. Deviations from randomness are often plainly evident in a visual inspection of the data in question. For example, we can examine the distribution of characters in our POTP using
ent -c POTP | head -97 | tail -94 | awk '{print $3}'> hist.dat
Plotting these values yields a histogram of the character distribution:
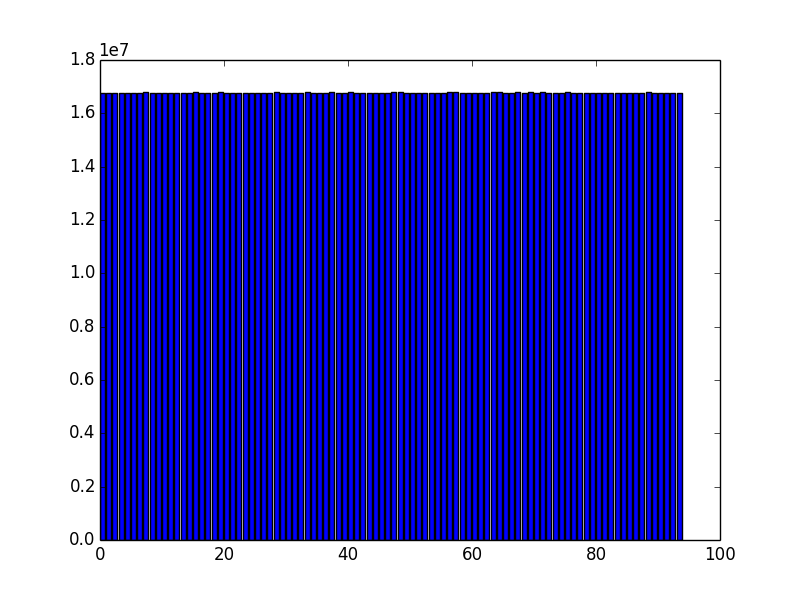
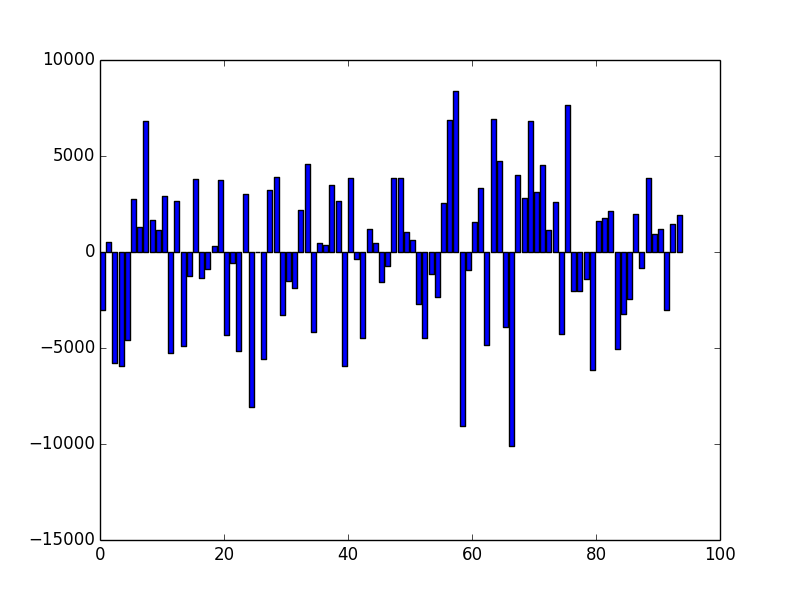
Looks almost entirely equally distributed, as we had hoped. However, in a finite random sequence, fluctuations do occur which can be made visible by plotting the deviation of each value from the mean of the distribution. Besides the fact that the values are small (the standard deviation is indeed only 0.02%), these deviations do not form any obvious pattern, but look indeed random.
We can perform the same analysis for the data after being encrypted by the Vigenère routine:
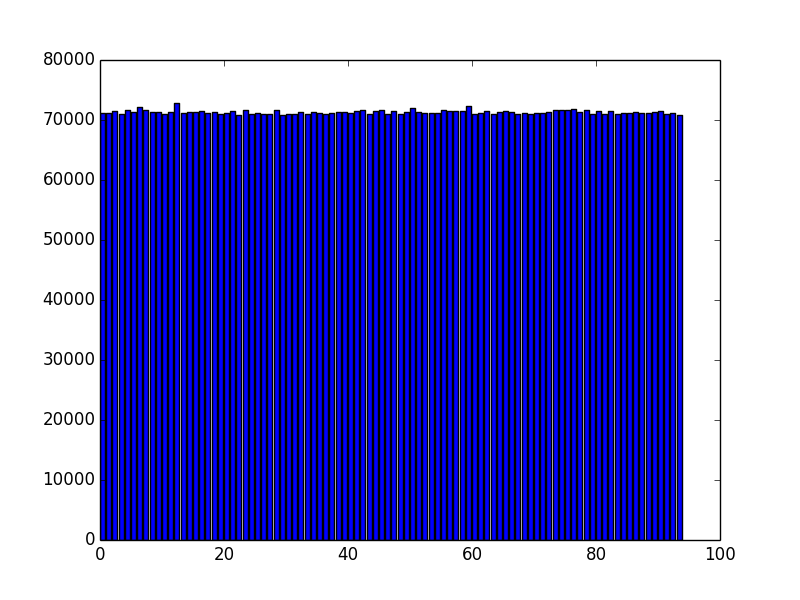
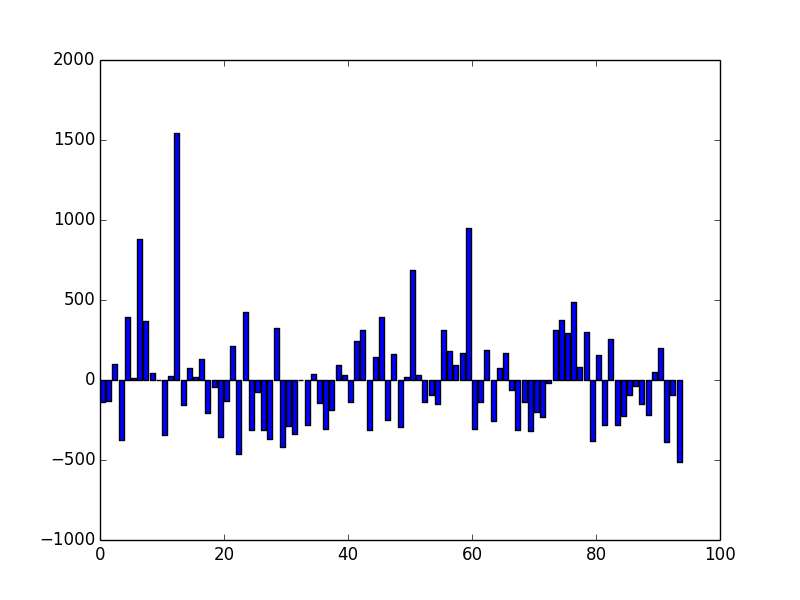
The fluctuations are larger (standard deviation 0.4%) since the sample size is significantly smaller, but once again the data do not exhibit any obvious deviations from a random distribution.
To analyze these data, by the way, I've used only the ipython console (ipython --pylab) and a few pylab commands:
a=loadtxt('hist.dat') n=arange(94) bar(n,a) bar(n,a-mean(a)) std(a)/mean(a)
For sake of clarity and documentation, I've attached an archive containing the shell script hfwcc and the Pascal routine vig.pas. For the former, I've disabled truncation as this feature forfeits local testing (it should only be used with two independent POTPs). For convenience, I've included a 64 bit binary of the latter compiled with fpc 2.6.2. The encoding tool base91, the random number generator csnrg and the analysis program ent are all available in the AUR (Arch User Repository). I'd expect you'll also get them for Debian, but users of other distributions will probably have to compile them themselves.