NumericQ

Mathematica is best known as a computer algebra system and its corresponding capabilities in symbolic computation. In recent years, however, Wolfram has implemented huge improvements in terms of raw speed in numerical computations. In my daily work, I found that Mathematica now often outperforms dedicated numerical systems such as Matlab.

In this context, a particularly convenient feature of Mathematica is how it's handling numerical objects. The following integral, for example, cannot be expressed in closed analytical form.

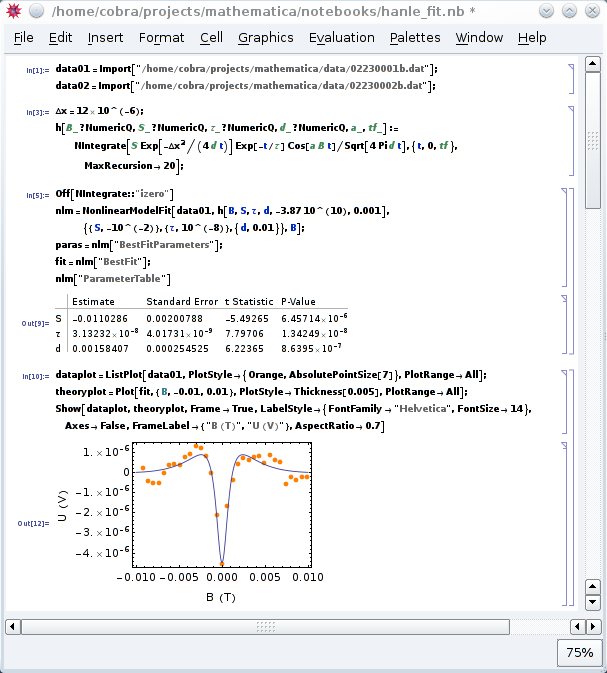
$ U(B) = S \int_0^\infty dt \exp(-\Delta x^2/4 D t) \exp(-t/\tau) \cos(g \mu_B B t/\hbar)/ \sqrt{4 \pi D t} $

Yet, it is still easily possible to use it in fitting experimental data:

To compute the integral itself takes about 150 ms on my humble E6600. The fit to 32 datapoints takes about 60 s, and the plot 15 s (as indicated in the notebook). To obtain the result (the non-local electrical Hanle effect) experimentally, well, that took our student a year. Which is why we emptied a bottle Moët & Chandon after the measurement. 😊